Die Grundaufgabe: Zeichne drei Geraden g, h und l. Konstruiere alle Strecken gegebener Länge s parallel zu g, deren Endpunkte P auf h und Q auf l liegen.
Lösungsstrategie: Es handelt sich wieder um eine Inzidenzaufgabe. Dazu lassen wir eine der drei Bedingungen der Aufgabe, nämlich daß Q auf l liegen müsse, weg und konstruieren die Ortslinie der Punkte Q, wenn P auf h wandert.
|
Die Konstruktionsvorschrift dazu lautet: (1) Die Geraden g, h und l ("Gerade") zeichnen (2) Eine Strecke der Länge s zeichnen ("Strecke") (3) Eine Strecke [PQ] so konstruieren
- Einen Punkt P an beliebiger Stelle auf h
- Die Parallele durch P zu g zeichnen
- Einen Richtungspunkt R auf die Parallele |
 |
die gegebene Strecke von P aus in Richtung R übertragen (Makro Streckenübertragung),
den Endpunkt Q nennen. Parallele und Richtungspunkt ausradieren.
(4) Die Option Ortslinie aufrufen, Q anklicken, P greifen und auf h wandern lassen.
In Bezug auf P ist der Punkt Q der Bildpunkt einer Verschiebung in Richtung g um den Betrag s. Die Ortslinie von Q ist also die Bildgerade h' von h bei dieser Verschiebung. Der Punkt Q ist demnach der Schnittpunkt der Bildgeraden h' mit der Geraden l. Den Punkt P erhält man dann durch Verschieben von Q mit der Umkehrabbildung (Umkehrpfeil!). Es gibt zwei Lösungs-Strecken entsprechend den beiden möglichen Orientierungen des Schiebepfeils.
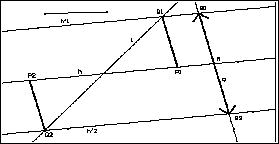
Aus der Lösungsstrategie ergibt sich die Konstruktionsvorschrift:
(1) Die Geraden g, h ("Gerade") und l ("Gerade durch 2 Punkte") zeichnen
(2) Eine Strecke gegebener Länge s zeichnen ("Strecke")
(3) Die beiden Schiebepfeile so konstruieren:
- Die Geraden g und h schneiden ("Schnitt"), den Schnittpunkt A nennen
- Auf g von A aus in beiden Richtungen Richtungspunkte R1 und R2 legen ("Punkt auf Objekt"),
- von A aus in Richtung R1 und R2 die gegebene Strecke der Länge s übertragen
(Makro Streckenübertragung), die Endpunkte Q1 und Q2 nennen
- Zur Verdeutlichung: Schiebepfeile von A nach B1 und nach B2 zeichnen (Makro Pfeil)
(4) Die Lösungs-Strecken so konstruieren:
- Gerade h mit beiden Schiebepfeilen verschieben (Makro Verschieben-Gerade),
die Bildgeraden h'1 und h'2 nennen
- Geraden h'1 und h'2 mit der Geraden l schneiden ("Schnitt"), die Schnittpunkte Q1 und Q2 nennen
- Punkte Q1 und Q2 mit der Umkehrabbildung (Umkehrpfeil!) abbilden (Makro Verschieben),
die Bildpunkte P1 und P2 nennen
- Die Strecken [P1Q1] und [P2Q2] zeichnen. Sie sind die gesuchten Lösungs-Strecken.
|
Zur Fallunterscheidung drehen wir die Gerade l, variieren die Länge s und finden: Sind h und l nicht parallel, so gibt es stets 2 Lösungen. Sind h und l parallel, so gibt es für h'¹l keine, für h'=l beliebig viele Lösungen. |
 |
Die erste Variation der Grundaufgabe: Die Gerade l wird durch einen Kreis l ersetzt.
|
Zur Konstruktion: Der Punkt A ist beliebig auf der Geraden g wählbar; von ihm aus werden Pfeile nach beiden Seiten angetragen. (In dem hier abgebildeten Beispiel muß dann nur nach einer Seite geschoben werden.) Zur Fallunterscheidung verschieben wir die Gerade h, variieren die Länge s und stellen fest: Es gibt 4, 3, 2, 1 oder keine Lösung je nachdem, ob die Geraden h'1 und/oder h'2 den Kreis l schneiden, berühren oder meiden. |
 |
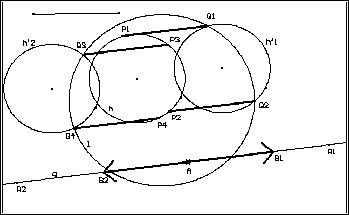
Die zweite Variation der Grundaufgabe: Die Geraden h und l werden beide durch Kreise ersetzt, die wir wieder h ("Kreis") und l ("Kreis aus Kreismittelpunkt und Kreispunkt") nennen.
Zur Konstruktion: Liegt der Kreis h im Äußeren des Kreises l, so braucht er nur auf eine Seite verschoben zu werden; liegt er im Inneren, so wird er nach beiden Seiten (entsprechend den beiden Schiebepfeilen) verschoben.
|
Zur Fallunterscheidung: Den Kreis h (Mittelpunkt und Kreispunkt) stetig verändern, den Kreis l verschieben. Man erkennt: Es gibt 4, 3, 2, 1 oder keine Lösung je nachdem, ob die Kreise h'1 und/oder h'2 den Kreis l schneiden, berühren oder meiden. |
 |