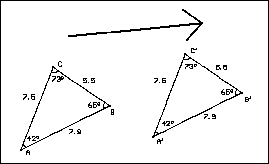
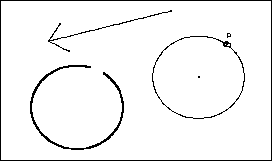Wir messen Seiten und Eckenwinkel, variieren den Schiebepfeil (Betrag, Richtung und Orientierung) und das Urdreieck und beobachten dabei: Ur- und Bildgeraden sind stets gleichlang, Ur- und Bildwinkel sind stets gleichgroß, Ur- und Bilddreiecke sind deshalb stets kongruent.
Die Verschiebevorschrift ist längentreu und winkeltreu, sie bildet Dreiecke auf kongruente Dreiecke ab. Die Verschiebevorschrift ist eine Kongruenzvorschrift.
- Jetzt verschieben wir eine Gerade (zwei Punkte der Gerade verschieben und durch die Bildpunkte eine Gerade zeichnen) und entwickeln daraus das Makro Verschieben-Gerade:
Eingabeobjekte: Anfangs- und Endpunkt des Schiebepfeils, zwei Punkte der Urgeraden g
Zielobjekte: Bildgerade g'