Es soll das Spiegelbild eines Kreises nach Gestalt und Lage bestimmt werden. Dazu verwenden wir die zweischrittige Ortslinien-Strategie. Der 1. Schritt geht so:
|
(1) Die Spiegelgerade a zeichnen ("Gerade") (2) Den Urkreis k zeichnen ("Kreis") (3) Die Bildfigur so markieren: - Einen Punkt P auf k legen ("Punkt auf Objekt") -
Die Option Ortslinie aufrufen,
den Punkt P' anklicken, |
 |
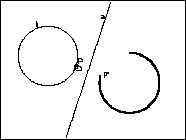Wir vermuten: Das Bild des Kreises k ist ein Kreis k'; der Mittelpunkt M' von k' ist das Bild des Mittelpunktes M von k, die Radien von Ur- und Bildkreis sind gleichgroß. Im 2. Schritt fahren wir also so fort:
(4) Beim Kreis k den Mittelpunkt M ("Kreismittelpunkt") und einen Kreispunkt K ("Punkt auf Objekt") hinzufügen
(5) Den vermuteten Bildkreis k' so konstruieren:
- Die Punkte M und K an a spiegeln, (Makro Geradenspiegeln), die Bildpunkte M' und K' nennen
- Den Kreis um M' durch K' zeichnen ("Kreis aus Kreismittelpunkt und Kreispunkt") und k' nennen
(Wegen der Längentreue der Spiegelvorschrift ist sein Radius |M'K'|=|MK|)
(6) Die Option Ortslinie nochmals aufrufen und damit das Bild des Kreises k markieren.
Wir sehen, daß sich der konstruierte Kreis k' und der mit der Option Ortslinie markierte Kreis decken. K' ist also das Bild von k, k' ist der Bildkreis von k. (Die markierte Kreislinie kann jetzt gelöscht werden.) Die Spiegelvorschrift ist kreistreu.
Aus der Konstruktionsvorschrift des Kreises k' entwickeln wir das Makro Geradenspiegeln-Kreis:
Eingabeobjekte: Spiegelgerade a, Kreismittelpunkt M und Kreispunkt K des Urkreises
(in dieser Reihenfolge)
Zielobjekt: Bildkreis
Mit diesem Makro läßt sich nicht nur (wie eben durchgeführt) ein "Kreis" mit "Kreismittelpunkt" und Kreis-"Punkt auf Objekt", sondern auch ein "Kreis aus Kreismittelpunkt und Kreispunkt" spiegeln.
Schließlich variieren wir den Urkreis stetig nach Lage und Größe (den "Kreis" bzw. beim "Kreis aus Kreismittelpunkt und Kreispunkt" den Mittelpunkt und den Kreispunkt mit der Zughand greifen) und beobachten Ur- und Bildkreise. Dabei kann man drei Fälle unterscheiden: Der Urkreis schneidet, berührt oder meidet die Spiegelgerade. Alle Kreise, deren Mittelpunkte auf der Spiegelgeraden liegen, sind Fixkreise.