Zweite Folgerung aus der Längentreue: Die Kongruenz von Ur- und Bilddreieck und die Winkeltreue

Es sollen beim Geradenspiegeln sowohl Ur- und Bilddreieck und auch Ur- und Bildwinkel verglichen werden. Dazu spiegeln wir ein Dreieck:

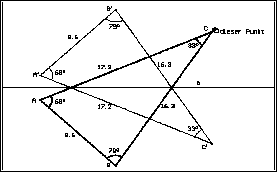
(1)   Die Spiegelgerade a zeichnen ("Gerade") (2) Ein Urdreieck ABC zeichnen ("Dreieck") (3) Das Bilddreieck konstruieren:      Das Urdreieck an a spiegeln (Makro Geradenspiegeln-Dreieck), das Bilddrei­eck A'B'C' nennen (4)   Die Stücke des Ur- und Bilddreiecks messen:      -  Die Seitenlängen messen ("Messung")      -  Die Eckenwinkel markieren ("Winkelmarkierung") und messen ("Messung")

Die eine oder andere Ecke des Urdreiecks greifen und in der Zeichenebene wandern lassen, dabei die Streckenlängen und Winkelweiten von Ur- und Bilddreieck beob­achten. Wir sehen:

-   Für jedes Urdreieck sind entsprechende Seiten von Ur- und Bilddreieck gleichlang. (Das liegt an der Längentreue der Spiegelvorschrift.) Ur- und Bilddreiecke haben deshalb dieselbe Form  und Größe; man sagt, sie sind deckungsgleich (kongruent). Die Spiegel­vorschrift bildet Dreiecke auf kongruente Dreiecke ab.

-   Für jedes Urdreieck sind entsprechende Winkel von Ur- und Bilddreieck gleichweit. (Das liegt an der Deckungsgleichheit der Dreiecke.) Die Spiegelvorschrift ist winkeltreu.