Geradenspiegeln ist eine Kongruenzvorschrift

Weil beim Spiegeln an Geraden jede Gerade wieder auf eine Gerade abgebildet wird, werden auch Strecken wieder auf Strecken abgebildet. Wie aber wirkt sich das Spiegeln auf die Streckenlänge aus?

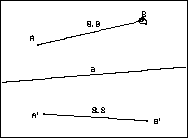
(1) Eine Spiegelgerade a zeichnen (2) Eine Urstrecke [AB] zeichnen ("Strecke") (3) Die Bildstrecke konstruieren:      -  Die Punkte A und B an a spiegeln (Makro         Geradenspiegeln), die Bildpunkte A' und B' nennen      -  Die Strecke [A'B'] zeichnen (4) Ur- und Bildstrecke messen ("Messung")

Die Strecke(nlänge) variieren (den Punkt A oder B mit der Zughand greifen und auf der Zeichenebene frei wandern lassen), dabei die Längenmaße vergleichen. Die Messung ist nur auf Millimeter genau. Im Rahmen dieser Meßgenauigkeit können wir vermuten, daß Ur- und Bildstrecken stets gleichlang sind. Wir nehmen an (das ist eine unbeweisbare Annahme, ein Axiom,), daß auch bei einem idealen Meßwerkzeug (das es in Wirklichkeit nicht gibt) die Maßzahlen von Ur- und Bildstrecke gleich wären. Mit dieser Annahme heben wir die Geometrie aus dem rein praktischen Umgang mit Zirkel und Lineal bzw. Geodreieck auf die gedankliche Ebene und damit die der Mathematik.

Deshalb nennt man die Spiegelvorschrift eine längentreue Vorschrift oder kurz eine Kongruenzvorschrift. Sie ist, wie wir später sehen werden, nicht die einzige Kongru­enzvorschrift. Deshalb ist "Kongruenzvorschrift" mehr als nur ein neuer Name.