Drei weitere ergebnisgleiche Spiegelvorschriften

Wenn wir die Spiegelvorschriften nach dem verwendeten Hilfsmittel benennen, so können wir bei der bisher benutzten Vorschrift, bei der im Unterricht gewöhnlich das Geodreieck verwen­det wird, von der Geodreieck-Vorschrift sprechen. Entsprechend wollen wir bei den drei folgenden Vorschriften verfahren, bei denen wir das Spiegeln mit anderen Werkzeugen durchführen werden.

Die Zirkel-Lineal-Vorschrift.

Aufgabe: Gegeben sind eine Spiegelgerade a (Lineal!) und ein Urpunkt P. Der Bildpunkt P' soll allein mit dem Zirkel konstruiert werden.

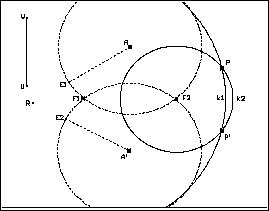
Lösungsstrategie: Es werden auf der Spiegelgeraden zwei Punkte (Fixpunkte) F1 und F2 markiert und mit ihnen als Mittelpunkte Kreise durch P gezeichnet. Der zweite Schnittpunkt der beiden Kreise ist der Bildpunkt P'. Die Punkte F1 und F2 kann man entweder beliebig auf a markieren oder als Schnittpunkte eines hinreichend großen Kreises um P mit der Spiegelgeraden a konstruieren. Die Abbildungsvorschrift lautet also:

(1)   Die Spiegelgerade a zeichnen      ("Gerade") (2) Einen Urpunkt P zeichnen ("Punkt") (3) Die zwei Fixpunkte so konstruieren:      -  Linke Zeichnung: Zwei beliebige    Punkte F1 und F2 auf a zeichnen    ("Punkt auf Objekt")

Wichtig ist zu erkennen, daß diese Konstruktionen unabhängig von der Wahl der darin vor­kommenden Parameter (links die Stellen von F1 und F2, rechts der Radius von k) zu einem gegebenen Urpunkt stets ein und denselben Bildpunkt als Ergebnis liefern. Dazu greift man bei der linken Zeichnung den Punkt F1 und/oder F2 mit der Zughand, läßt ihn auf a wandern und beobachtet P'. Bei der rechten Zeichnung greift man den Punkt F1 mit der Zughand, läßt ihn auf a wandern und beobachtet P'.

Schließlich kann man auch den Punkt P mit der Zughand greifen, auf der Zeichenebene wandern lassen und den Bildpunkt beobachten.

1. Anmerkung: Für diese Konstruktionsvorschriften lassen sich allerdings keine Makros definieren, da "beliebig" kein für den Cabri Géomètre definierbarer Begriff ist.

2. Anmerkung: Will man, wie hier gezeigt, der Übersichtlichkeit wegen eine Gerade nicht von Seitenrand zu Seitenrand zeichnen, so lege man zwei Punkte auf sie, zeichne die Strecke zwischen den beiden Punkten und radiere zuletzt die Gerade und die beiden Punkte aus.

Die Zirkel-Vorschrift

Aufgabe: Gegeben sind ein Urpunkt A und sein Bildpunkt A'. Zu einem beliebigen Punkt P der Zeichenebene soll der Bildpunkt P' allein mit dem Zirkel konstruiert werden.

Lösungsstrategie: Zuerst konstruieren wir zwei Fixpunkte F1 und F2 und verfahren dann weiter wie oben. Die Fixpunkte erhalten wir als Schnittpunkte zweier hinreichend großer Kreise um A und A' mit gleichem Radius.

Die Abbildungsvorschrift lautet dann:

(1) Zwei Punkte A und A' zeichnen ("Punkt")

(2) Einen Urpunkt P zeichnen ("Punkt")

(3) Die zwei Fixpunkte so konstruieren:

     -  Um A und A' Kreise mit gleichem Radius, die sich schneiden, wie folgt zeichnen:

        (a) Eine Strecke [UV] zeichnen, für die |UV|>|AA'|:2 ist ("Strecke")

        (b) Einen Richtungspunkt R zeichnen, die Strecke [UV] von A und von A' aus in Richtung R
   übertragen (Makro Streckenübertragung), die Endpunkte E1 und E2 nennen

        (c) Die Kreise um A durch E1 und um A' durch E2 zeichnen

        ("Kreis aus Kreismittelpunkt und Kreispunkt")

        (d) Die beiden Kreise schneiden (Schnitt"), die Schnittpunkte F1 und F2 nennen

        (f) Die Hilfslinien (Radiusstrecken samt Endpunkten E1 und E2, Kreise um A und A') ausradieren
   ("Radiergummi")

(4) Den Bildpunkt wie bei der Zirkel-Lineal-Vorschrift konstruieren.

Wichtig ist es wieder zu erkennen, daß der Bildpunkt unabhängig vom Parameter der Abbildungs­vorschrift (das ist die Strecken­länge |UV|) ist. Dazu den Punkt U oder V mit der Zughand greifen, die Länge von [UV] variieren und den Bildpunkt beobachten. Auch den Urpunkt P greifen und variieren. Sonderfälle: P=A, P=A', P=P' (Fixpunkt, die beiden Kreise k1 und k2 berühren sich). Zuletzt noch den Punkt A' greifen und auf der Zeichenebene wandern lassen. Auch diese Vorschrift ist in der vorliegenden Fassung für die Definition eines Makro ungeeignet, weil die Bedingung |UV|>|AA'|:2 für den Radius der Kreise keine eindeutige Festlegung beinhaltet. Doch läßt sich ein solcher Radius mit |UV|=|AA'| eindeutig definieren, so daß man die Vorschrift damit leicht "makro-tauglich" machen kann:

Hieran anschließend kann man das Makro Zirkelvorschrift definieren:

Wir machen uns bewußt: Um ein Makro definieren zu können, muß der Konstruktionsweg von den Eingabe- zu den Zielobjekten bei jedem Schritt eindeutig sein. Auch für die Definition von Makros muß man Strategien entwickeln.

.Die Lineal-Vorschrift

Aufgabe: Gegeben sind eine Spiegelgerade a, ein Punkt A und sein Bildpunkt A', außerdem ein Urpunkt P. Der Bildpunkt P' soll allein mit dem Lineal konstruiert werden.

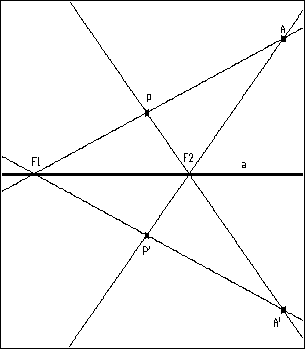
Lösungsstrategie: Die Bilder der Geraden AP und A'P schneiden sich (wegen der Wechsel­seitigkeit der Spiegelvorschrift) im Bildpunkt P'.

Damit lautet die Abbildungsvorschrift:

(1)   Die Spiegelgerade a zeichnen ("Gerade")      Den Punkt A ("Punkt") und      den Punkt A' zeichnen      (Makro Geradenspiegeln) (2)   Einen Urpunkt P zeichnen ("Punkt") (3)   Den Bildpunkt so konstruieren:      -  Die Geraden AP und A'P zeichnen    ("Geraden durch 2 Punkte")      -  Diese Geraden mit a schneiden    ("Schnitt"), die Schnittpunkte F1 bzw    F2 (Fixpunkte) nennen      -  Die Bildgeraden A'F1 und AF2    zeichnen ("Geraden durch 2 Punkte")      -  Die Bildgeraden schneiden ("Schnitt")

Im Grunde handelt es sich auch hier wieder darum, die gegebene Figur symmetrisch zu ergänzen. Dahinter steckt die Wechselseitigkeit der Spiegelvorschrift.

Wir greifen den Urpunkt P mit der Zughand und verschieben ihn auf der Zeichenebene (Bildschirm). Man sieht: Im Falle, daß P ein Punkt der Geraden AA' oder der Parallelen zu a durch A ist, versagt die Konstruktion. Dann muß man

-   zunächst einen Hilfspunkt B wählen, die Geraden AB und BP zeichnen und B so ver­schieben, daß beide Geraden die Spiegelgerade auf dem Zeichenblatt schneiden,

-   den Bildpunkt B' mit der Lineal-Vorschrift, bezogen auf A und A' konstruieren, und dann

-   den Bildpunkt P' mit der Lineal-Vorschrift, bezogen auf B und B' konstruieren.

Die Lineal-Vorschrift läßt sich, sofern man keinen Hilfspunkt B benötigt, ohne weiteres als Makro Linealvorschrift definieren, da alle Konstruktionsschritte eindeutig sind. Benötigt man einen Hilfspunkt, so wendet man das Makro zweimal nacheinander an.

Vier Vorschriften - Eine Abbildung

Es soll eine Urfigur mit einer der vier Vorschriften gespiegelt werden. Dann sollen alle für die Vorschrift benötigten Linien ausradiert ("Radiergummi") werden und nur die Ur- und Bildfigur sichtbar bleiben. Niemand kann an Hand der beiden Figuren erkennen, welche der vier Vorschriften zum Spiegeln benutzt wurde. Denn alle vier Vorschriften liefern zu jedem Urpunkt als Ergebnis stets ein und denselben Bildpunkt. Wir sagen: Die vier Vorschriften sind ergebnisgleich. Alle ergebnisgleichen Vorschriften liefern dieselbe Abbildung von Ur- und Bildpunkt, wir nennen sie Geradenspiegelung.

Zum Konstruieren des Bildpunktes ist es also gleichgültig, welche der ergebnisgleichen Vor­schriften man benutzt, man erhält immer dieselbe Abbildung. Gewöhnlich verwendet man die Geodreieck-Vorschrift bzw. das Makro Geradenspiegeln, es ist die Standardvorschrift der Geradenspiegelung. - Würde man auch noch die Spiegelgerade ausradiert haben, so könnte man sie rekonstruieren: Sie ist die Mittelsenkrechte der Verbindungsstrecke beider Punkte ("Mittelsenkrechte").