Die Streifentreue der Geradenspiegelung
Wir haben bisher schon viele Eigenschaften der Standardvorschrift
kennengelernt (Fixeigenschaften, Geradentreue, Kreistreue, ...). Alle zu ihr
ergebnisgleichen Vorschriften haben naturgemäß diese selben Eigenschaften. Es
sind also nicht nur Eigenschaften einer einzigen Vorschrift, sondern Eigenschaften
der Geradenspiegelung (der Abbildung).
Streifen: Von zwei sich schneidenden Geraden (bzw. zwei von einem Punkt
ausgehenden Halbgeraden) berandete Flächenstücke kennen wir unter der Bezeichnung
"Winkel". Wir haben Winkel an einer Geraden gespiegelt und dabei festgestellt,
daß die Geradenspiegelung winkeltreu ist. Von zwei parallelen Geraden
berandete Flächenstücke nennt man Streifen. Auch bei ihnen fragen wir
nach ihrem Bild bei der Geradenspiegelung (die wir durch ihre Standardvorschrift
repräsentieren).
Streifen
parallel und senkrecht zur Spiegelgeraden
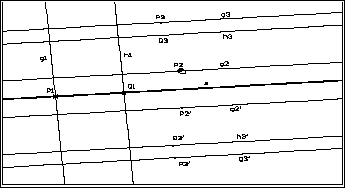
Zuerst zeichnen wir Streifen, deren Randgeraden parallel
oder senkrecht zur Spiegelgeraden sind. Wie wir dabei sehen, gibt es sogar Fixstreifen:
|
Alle Streifen
senkrecht zur Spiegelgeraden sind Fixstreifen.
- Alle Streifen,
deren Randgeraden parallel und symmetrisch zur Spiegelgeraden liegen,
sind Fixstreifen.
Wir greifen die Punkte P und Q, durch die die Senkrechten
bzw. Parallelen verlaufen, mit der Zughand und verschieben damit die Randgeraden
parallel. Auf diese Weise wird die Streifenbreite verändert, doch werden
die Urstreifen stets wieder auf (sogar gleichbreite, also kongruente!)
Streifen, die Bildstreifen, abgebildet.
|
 |
Streifen
weder senkrecht noch parallel zur Spiegelgeraden
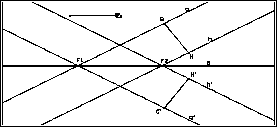
Schließlich bilden wir einen Streifen ab, dessen Randgeraden
weder senkrecht noch parallel zur Spiegelgeraden verlaufen.
(1) Die Spiegelgerade a zeichnen ("Gerade")
(2) Die Randgerade g des Urstreifens
konstruieren:
-
Einen Punkt auf a legen ("Punkt auf Objekt") und F1 nennen
-
Eine Gerade g durch F1 und einen weiteren Punkt G zeichnen ("Gerade durch
2 Punkte")
(3) Den Abstand der Randgeraden g und
h des Urstreifens festlegen:
-
Die Senkrechte in G auf g konstruieren ("Lot/Senkrechte")
-
Eine Strecke zeichnen ("Strecke")
-
Einen Richtungspunkt R auf die Senkrechte legen ("Punkt auf Objekt")
und die Strecke von G aus in
Richtung R übertragen (Makro Streckenübertragung), den Endpunkt H nennen,
Senkrechte und
Richtungspunkt R ausradieren ("Radiergummi")
(4) Die Randgerade h des Urstreifens
konstruieren: Die Parallele durch H zu g konstruieren (Parallele")
(5) Die Bilder der Geraden g und h
und der Abstandsstrecke [GH] konstruieren:
-
Den Fixpunkt der Geraden h konstruieren ("Schnitt") und F2 nennen
-
Die Geraden g und h an a spiegeln (Makro Geradenspiegeln-Gerade)
-
Die Punkte G und H an a spiegeln (Makro Geradenspiegeln) und G' bzw H' nennen,
die
Strecke [G'H'] zeichnen
|
Wegen der Längentreue der Geradenspiegelung ist |G'H'|=|GH|,
das Bild des Urstreifens mit den Randgeraden g und h ist also wieder
ein Streifen (der Bildstreifen) mit den Randgeraden g' und h'. Ur- und
Bildstreifen sind sogar kongruent.
Die Parameter, mit deren Hilfe wir die Figur
verändern können, sind die Länge der Abstandsstrecke (Endpunkt der gegebenen
Strecke mit der Zughand greifen und ziehen) und die Randgerade g (den
Punkt G mit der Zughand greifen und die Gerade um F1 drehen). Als Sonderfälle
erhält man die Fixstreifen senkrecht zur Spiegelgeraden. Die Streifen
parallel zur Spiegelgeraden erhält man nur dann als Sonderfälle, wenn
man F1 von a und F2 von a und h löst ("Verbindung aufheben"),
anschließend F2 an h bindet ("Objektbindung eines Punktes")
und außer G jetzt auch F1 mit der Zughand greift und variiert.
|
 |
Die Geradenspiegelung bildet Streifen auf kongruente Streifen
ab. Wir sagen: Die Geradenspiegelung ist streifentreu.
Statt von Streifentreue spricht man auch von Parallelentreue:
Parallele Urgeraden g||h werden auf parallele Bildgeraden g'||h' abgebildet.

