Eine Aufgabenfamilie

Die Aufgabenfamilie besteht aus einer Grundaufgabe mit zwei Variationen und einer Abwandlung der Grundaufgabe mit entsprechenden Variationen. Dabei wird die Drehvorschrift als Konstruktionsmittel eingesetzt.

Die Grundaufgabe: Gegeben sind ein Punkt A und zwei Geraden b und c. Gesucht ist ein gleichseitiges Dreieck, dessen eine Ecke A ist und dessen Ecken B und C auf b bzw. c liegen.

Lösungsstrategie: Bei allen Inzidenz-Aufgaben (das sind Aufgaben, bei denen Punkte an Objekte gebunden werden, "Objektbindung eines Punktes") geht man in der heuristischen Phase so vor, daß man zunächst eine der Inzidenzbedingungen wegläßt und mit dem Cabri Géomètre die Ortslinie für diesen dann freien Punkt konstruiert, wofür man eine zweite Inzidenzbedingung variabel gestaltet. (Strategie für Inzidenzaufgaben)

Für die vorliegende Aufgabe bedeutet das: Die Ecke A des gleichseitigen Dreiecks liegt fest, die Ecke B ist auf der Geraden b variabel und die Ecke C ist frei. Gefragt ist nach der Orts­linie für C, wenn B die Gerade b durchläuft. Wir konstruieren also zunächst:

(1) Den Punkt A ("Punkt") und die Geraden b und c ("Gerade") zeichnen

(2) Ein gleichseitiges Dreieck so konstruieren:

     -  Einen Punkt auf b legen ("Punkt auf Objekt") und B nennen

     -  Mit den Punkten A und B ein gleichseitiges Dreieck ABC zeichnen (Makro gleichseitiges Dreieck)
   Es gibt 2 Möglichkeiten je nach der Reihenfolge, in der die Ecken A und B angeklickt werden.

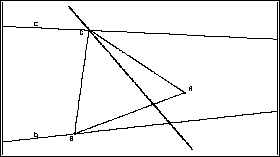
Ruft man die Option Ortslinie auf, klickt den Punkt C an und greift den Punkt B, so stellt C den Bildpunkt von B bei Drehung um A mit 60 Grad (Eckenwinkel des gleichseitigen Dreiecks in A) dar. Dies gilt für jeden Punkt B auf b. Läßt man deshalb den Punkt B die Gerade b durchlaufen, so markiert C die Bildgerade b' von b beim Drehen um A mit 60 Grad. Daraus ergibt sich das Konstruktionsverfahren für C: Der Punkt C ist der Schnittpunkt der Geraden c und der Geraden b', die aus der Geraden b durch Drehen um 60 Grad um den Punkt A hervorgeht. Die Konstruktionsvorschrift lautet:

(1) Den Punkt A und die Geraden b ("Gerade durch 2 Punkte") und c ("Gerade") zeichnen (2) Den Punkt C konstruieren:      -  Den Drehwinkel UVW von 6O Grad    zeichnen      -  Die Gerade b um A mit 6O Grad drehen    (Makro Drehen-Gerade)         Es gibt zwei Möglichkeiten, je nach dem    Drehsinn des Drehwinkels (UVW und WVU    anklicken), die Bildgeraden b1' und b2'    nennen      -  Die Geraden b1' und b2' mit c schneiden ("Schnitt"), die Schnittpunkte C1 und C2 nennen (3) Die gleichseitigen Dreiecke (Lösungsdreiecke) und den Punkt B konstruieren      -  Gleichseitige Dreiecke mit den Ecken A und C1 bzw. C2 und A konstruieren         (Makro gleichseitiges Dreieck)      -  Die dritten Eckpunkte B1 und B2 benennen.

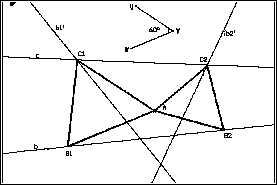Fallunterscheidung: Gerade b (Gerade durch 2 Punkte!) drehen. Schließen b und c einen 6O-Grad-Winkel ein, so gibt es 1 Lösung, sonst gibt es stets 2 Lösungen.

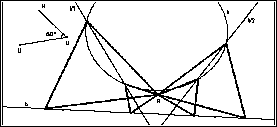
Erste Variation der Grundaufgabe: Die Gerade c wird durch einen Kreis k ("Kreis") ersetzt. Gesucht sind alle gleichseitigen Dreiecke, deren eine Ecke der gegebene Punkt A ist und deren andere Ecken B auf b und C auf k liegen. Die Lösungsstrategie ist dieselbe wie bei der Grundaufgabe. Zur Fallunterscheidung variieren wir die Parameter b (drehen) und/oder k (verschie­ben). Wir sehen: Es kann 4, 3, 2, 1 oder kein Lösungsdreieck geben, je nachdem, ob die Geraden b'1 und/oder b'2 den Kreis k schneiden, berühren oder meiden.

Zweite Variation der Grundaufgabe: Die Geraden b und c werden durch Kreise k und l ersetzt. Gesucht sind alle gleichseitigen Dreiecke, deren eine Ecke der gegebene Punkt A ist und deren Ecken B und C auf k und l liegen.

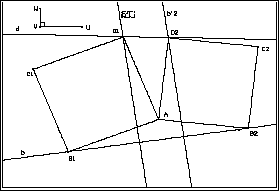
Weil der Kreis k (um A mit 6O Grad in beiden Richtungen) gedreht werden muß, müssen der Kreis­mittelpunkt und ein Kreispunkt gegeben sein. Zum Drehen wird das Makro Drehen-Kreis benötigt. Fallunterscheidung: Den Kreis k variieren und/oder den Kreis l verschieben. Es gibt O, 1, 2, 3 oder 4 Lösungsdreiecke, je nach­dem, ob die Kreise k'1 und/oder k'2 den Kreis k schneiden, berühren oder meiden. Abwandlung der Grundaufgabe: Statt für ein gleichseitiges Dreieck kann man die Grundaufgabe auch für ein Quadrat mit fester Ecke A und den Ecken B auf b und D auf d stellen. Das variable Quadrat so konstruieren: Einen Punkt B auf b legen ("Punkt auf Objekt"), das Quadrat mit den Ecken A und B zeichnen (Makro Quadrat aus benachbarten Ecken).

Die Option Ortslinie aufrufen, den Punkt D anklicken, den Punkt B greifen und auf der Geraden b wandern lassen. Der Punkt D ist in Bezug auf den Punkt B der um 90 Grad gedrehte Bildpunkt. Die Ortslinie von D für den auf b laufenden Punkt B ist also die Bildgerade b' senkrecht zu b.

Zur Fallunterscheidung (Gerade d drehen!):

-   Für b^d und b'¹d gibt es keine, für b'=d beliebig viele Lösungs-Quadrate;

-   sonst gibt es stets 2 Lösungs-Quadrate.

Diese abgewandelte Grundaufgabe kann natürlich auch wieder für Gerade und Kreis und für zwei Kreise umformuliert werden, das sind zwei weitere Aufgaben.