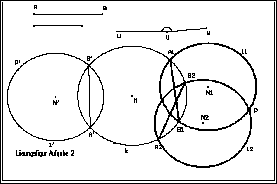
(1) Den Kreis k zeichnen ("Kreis )
Den Punkt
P im Innern des Kreises k zeichnen ("Punkt")
Eine Strecke
[AB] der gegebenen Länge s zeichnen ("Strecke")
(2) Eine beliebige Kreissehne der Länge s so konstruieren:
- Einen Punkt A' auf k legen ("Punkt auf Objekt")
- Den Hilfskreis h1 um A' mit Radius |AB| zeichnen
("Kreis aus Kreismittelpunkt und Radius")
- Die Kreise h1 und k schneiden ("Schnitt"), einen der Schnittpunkte
B' nennen
- Strecke [A'B'] zeichnen ("Strecke"), sie ist die gesuchte beliebige Kreissehne.
- Den Hilfskreis h1 und den 2. Schnittpunkt von
h1 und k ausradieren ("Radiergummi")
(3) Den Punkt P' auf der Kreissehne [A'B'] so bestimmen:
- Den Hilfskreis h2 um M durch P zeichnen ("Kreis aus Kreismittelpunkt und Kreispunkt)
- Kreis h2 und Sehne [A'B'] schneiden ("Schnitt"), einen der Schnittpunkte
P' nennen.
- Den Hilfskreis h2 und den zweiten Schnittpunkt
von h2 und [A'B'] ausradieren ("Radiergummi")
(4) Die eine Lösungs-Sehne so konstruieren:
- Einen zum Winkel P'MP gleichgroßen Winkel UVW
zeichnen (Makro Winkelübertragung),
dann einen
Punkt W auf den freien Schenkel legen,
Strecke [VW] zeichnen, den freien Schenkel ausradieren
- Die Gerade g' durch die Punkte A' und B' legen
("Gerade durch 2 Punkte")
- Die Gerade g' um M mit dem Winkel UVW drehen
(Makro Drehen-Gerade), die Bildgerade g1
nennen
- Gerade g1 und Kreis k schneiden, die Schnittpunkte
mit A1 und B1 bezeichnen
- Strecke [A1B1] zeichnen ("Strecke"), sie ist die eine Lösungs-Sehne.
- Gerade g' ausradieren ("Radiergummi")
|
(5) Die andere Lösungs-Sehne so konstruieren: - Die Gerade MP zeichnen ("Gerade durch 2 - Die Gerade g1 an der Geraden MP spie- - Gerade g2 und Kreis k schneiden - Die Strecke [A2B2] zeichnen ("Strecke"), - Geraden MP, g1 und g2 ausradieren ("Radiergummi"). |
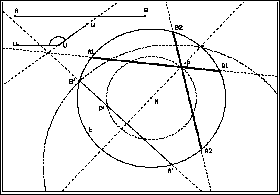 |