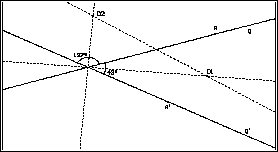
Lösung: Der Drehpunkt liegt auf der Mittelsenkrechten von [AA'] und auf einer Halbierenden der von g und g' gebildeten Winkel, ist also der Schnittpunkt dieser beiden Ortslinien. Es gibt 2 mögliche Drehvorschriften je nachdem, ob man die Drehung im Gegenuhrzeigersinn (hier im Beispiel D1, 137 Grad) oder im Uhrzeigersinn (D2, 43 Grad) durchführen will. Gibt man noch den Drehsinn der gesuchten Vorschrift vor, so ist die Lösung eindeutig.

Den Punkt A oder A' mit der Zughand greifen und auf g bzw. g' wandern lassen. Sonderfall: Sind A und A' gleichweit vom Schnittpunkt der Geraden g und g' entfernt, so gibt es genau einen Drehpunkt, nämlich diesen Schnittpunkt. Der Drehwinkel beträgt dann bei unserem Beispiel im Uhrzeigersinn 43 Grad, im Gegenuhrzeigersinn die Ergänzung zu 360 Grad.

(1) Zwei Geraden g,g' zeichnen ("Gerade")

(2) Die vier Punkte zeichnen:

     -  Die Punkte A,B auf g und den Punkt A' auf
   g' beliebig zeichnen ("Punkt auf Objekt")

     -  Die Strecke [AB] zeichnen ("Strecke")

     -  Einen Richtungspunkt R auf g' legen
   ("Punkt auf Objekt"). Von A' aus gesehen
   gibt es dafür zwei mögliche Richtungen.
   Entscheidet man sich für eine von beiden,
   so ist die Lösung eindeutig.