Drehsymmetrische Figuren
Es sollen Figuren gezeichnet werden, die man durch Drehen auf sich selbst
abbilden kann. (Deckabbildung).
Man nennt sie drehsymmetrische Figuren.
Wir beginnen damit, eine drehsymmetrische Figur aus Dreiecken zu zeichnen,
und wählen als Drehwinkel 60 Grad.
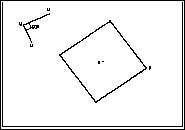
(1) Den Drehpunkt D und den Drehwinkel UVW zeichnen
(2) das Urdreieck ABC zeichnen
(3) Die drehsymmetrische Figur so konstruieren:
- Das Urdreieck um D drehen (Makro Drehen-Dreieck)
- Die folgenden Anweisungen 4mal nacheinander durchführen:
(a) Das
Bilddreieck als Urdreieck auffassen
(b) Das
Urdreieck um D drehen (Makro Drehen-Dreieck)
In der Anweisung (3) ist eine Zählschleife
(for-Schleife) eingebaut. Statt dessen hätte man auch eine Solange-Schleife
(While-Schleife) oder eine Wiederhole-Schleife (Repeat-Schleife)
formulieren können.
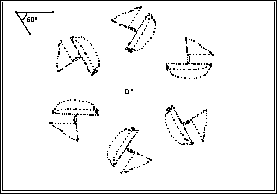
Die Figur besteht aus 6 Dreiecken. Sie wird durch Drehen um Vielfache von
60 Grad auf sich abgebildet, ist also drehsymmetrisch. Die Ecken des Urdreiecks
mit der Zughand greifen und das Dreieck (und damit die ganze Figur) variieren,
z.B. eine Ecke in den Drehpunkt legen,.......
Auch durch Freihandzeichnen können drehsymmetrische Figuren hergestellt
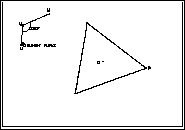
werden. Dazu ersetzen wir in der Konstruktionsvorschrift "Dreieck"
durch "Punkt" und fügen eine weitere Anweisung hinzu:
(4) Die Option
Ortslinie aufrufen, die Shift-Taste drücken
und nacheinander den Urpunkt und alle Bildpunkte anklicken, den Urpunkt
mit der Zughand greifen und mit dem Freihandzeichnen beginnen.
 |
 |
Regelmäßige
Vielecke
Wir führen die Konstruktionsvorschrift für drehsymmetrische Figuren noch
einmal durch. Dabei soll der Drehwinkel 30 Grad weit sein, es soll
ein Punkt abgebildet werden und bei der Zählschleife soll bis 10
gezählt werden. Zuletzt soll als weitere Anweisung hinzugefügt werden:
(4) Benachbarte Punkte durch Strecken verbinden. Es
entsteht ein regelmäßiges 12Eck.
Jetzt den Punkt U oder W des Drehwinkels UVW mit der Zughand greifen und
den Winkel stetig bis 180 Grad vergrößern. Dabei beobachten wir sich stetig
verändernde regelmäßige und unregelmäßige Vielecke, die einander abwechseln.
Wir notieren die regelmäßigen Vielecke und die Drehwinkel, bei denen sie auftreten:
Drehwinkel-Weite 30 45 60 72 90 120 180 Grad
regelmäßiges..... 12Eck 8Eck 6Eck 5Eck 4Eck 3Eck 2Eck
Zu jedem Teiler von 360 Grad gibt es ein regelmäßiges Vieleck (zu 15 Grad
gibt es das 24Eck). Das Produkt aus Eckenzahl und Drehwinkel-Weite ist immer
360 Grad. Alle regelmäßigen Vielecke sind drehsymmetrisch, die Drehwinkel-Weiten
der Deckabbildungen sind Vielfache der in der Tabelle angegebenen Weiten.
Für Drehwinkel, deren Weiten nicht Teiler von 360 Grad sind, gibt es keine
regelmäßigen Figuren.
Hier sind drei Momentaufnahmen abgebildet, die beim stetigen Vergrößern
des Drehwinkels festgehalten wurden: