Eine Aufgabenfamilie
Die Grundaufgabe: Gegeben sind ein Punkt P und zwei Geraden g und h.
Gesucht ist eine Strecke [AB], deren Endpunkte auf g bzw. h liegen und die durch
P halbiert wird.
Lösungsstrategie: Da P die gesuchte Strecke halbieren soll, kann man
P als Spiegelpunkt und die Punkte A und B als Ur- und Bildpunkte einer Punktspiegelung
auffassen (Punktspiegeln als Konstruktionsmittel). Da es sich außerdem
um eine Inzidenzaufgabe handelt, kann man die Strategie für Inzidenzaufgaben
anwenden: Eine der drei Bedingungen (die Bedingung für B) zunächst weglassen,
eine zweite (die Bedingung für A) variabel gestalten und die Ortslinie für den
freien Punkt (das ist der Punkt B, dessen Bedingung zunächst weggelassen wurde)
markieren. Also:
|
(1) Die Geraden
g ("Gerade"), h ("Gerade durch 2 Punkte")
und den Punkt P ("Punkt") zeichnen
(2) Eine Strecke [AB] so zeichnen:
- Einen Punkt auf g legen ("Punkt auf
Objekt") und A nennen
- A an P spiegeln (Makro Punktspiegeln),
den Bildpunkt B nennen
- Die Strecke [AB] zeichnen
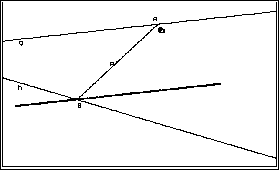
(3) Die Option Ortslinie
aufrufen, den Punkt B anklicken, den Punkt A greifen und auf g wandern
lassen.
|
 |
|
Der Punkt
B markiert die Bildgerade g' von g bei Punktspiegelung an P. Daraus ergibt
sich das Konstruktionsverfahren für B und A:
(4) Die Gerade
g' konstruieren (Makro Punktspiegeln-Gerade). Die Geraden h und g'
schneiden ("Schnitt"), den Schnittpunkt B nennen. B an P punktspiegeln
ergibt A.
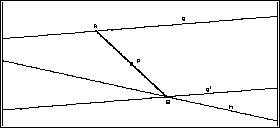
Zur Fallunterscheidung
variieren wir die Parameter g (verschieben), h (drehen) und P. Wir sehen:
- Ist g nicht
parallel zu h, so gibt es genau 1 Lösungs-Strecke,
- ist g parallel
zu h, so ist jede Strecke [AB] durch P eine Lösung, sofern P ein Punkt
der Mittelparallelen des von g und h gebildeten Streifens ist. Sonst gibt
es keine Lösung.
|
 |
Erste Variation
der Grundaufgabe:
Die Gerade h wird durch einen Kreis k ("Kreis")
ersetzt.
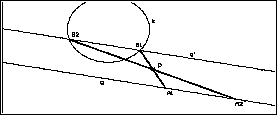
Zur Fallunterscheidung verändern wir g (drehen)
und/oder k (verschieben) stetig und stellen fest: Es gibt 2, 1 oder keine Lösung
je nachdem, ob sich g und k schneiden, berühren oder meiden.
Zweite Variation
der Grundaufgabe:
g und h werden durch Kreise k ("Kreis") und
l ("Kreis aus Kreism. u. Kreisp.) ersetzt.
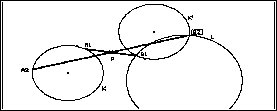
Zur Fallunterscheidung verändern wir k (verschieben)
und l stetig und stellen fest: Es gibt 2, 1 oder keine Lösung je nachdem, ob
sich k und l schneiden, berühren oder meiden. Für k'=l gibt es beliebig viele
Lösungen.
Dritte Variation
der Grundaufgabe: Es handelt
sich um eine Variante der 2-Kreis-Aufgabe. Die beiden Kreise k und l sollen
sich schneiden und P soll einer der beiden Schnittpunkte sein.
Vierte Variation
der Grundaufgabe: Die beiden
Geraden g und h der Grundaufgabe sollen sich auf dem Zeichenblatt schneiden.
Dann wird die Aufgabe gewöhnlich so formuliert: Gegeben ist ein Winkel und ein
Punkt P innerhalb des Winkels. Gesucht ist eine Strecke, deren Endpunkte auf
den Schenkeln des Winkels liegen und die durch P halbiert wird.
Wichtig für das Verstehen,
Befolgen und Erstellen von Abbildungs- und Konstruktionsvorschriften ist es,
ihre Struktur zu kennen und darin denken zu lernen. Sie läßt sich in den drei
Fragen Was? Wie? Womit? zusammenfassen.
- Was? - Zunächst muß man sich beim Lesen und
Befolgen oder Erstellen einer Vorschrift im klaren darüber
sein bzw. werden, welche Objekte (Punkt, Gerade, Kreis, .....) gezeichnet/konstruiert
werden sollen. Das ist
eine strategische Frage, also eine Frage im Zusammenhang mit der
Lösungsstrategie.
Oft wird man beim Erstellen einer Vorschrift
eine Überlegungsfigur dazu benötigen und auch nach Versuch
und Irrtum vorgehen müssen. ("Versuch und Irrtum" muß jetzt
nicht mehr in Gedanken, sondern kann mit
dem Cabri visuell auf dem Bildschirm durchgeführt werden!)
Die Antworten auf die Fragen "Was?"
bilden die im Text mit (1), (2), (3), ...... durchnumerierten Konstruktionsziele.
Sie stellen damit Überschriften für Teilprogramme dar; jede Vorschrift
ist also in Teilprogramme gegliedert.
- Wie? - Zum Befolgen oder Erslellen eines
Teilprogramms muß man wissen, auf welchem Weg das im
Konstruktionsziel genannte Objekt konstruiert werden kann. Die Frage "Wie?"
ist demnach eine taktische
Frage.
Beim Erstellen einer Vorschrift wird
man den zum Ziel führenden Konstruktionsweg oft mit Versuch und
Irrtum finden müssen, wobei sich die Fragen nach Ziel und Weg gegenseitig
bedingen können, weil ja auch
die Gegebenheiten des Werkzeugs einfließen.
Im Text der Abbildungs- und Konstruktionsvorschriften
handelt es sich bei den Antworten auf die Frage
"Wie?" um die Folgen von mit Spiegelstrichen versehenen
Handlungsanweisungen; sie sind gegenüber den
numerierten Überschriften eingerückt.
- Womit? - Diese Frage bezieht sich auf das
Werkzeug, beim Cabri also auf die Option, die aufgerufen werden
muß, um eine bestimmte Handlungsanweisung durchführen zu können.. Es handelt
sich damit um eine
handwerkliche Frage.
In diesem Buch sind die Antworten auf
die Fragen "Womit?" in kursiver Schrift in Klammern jeder
Handlungsanweisung hinzugefügt.
Durchführen
und Erstellen von Abbildungs- und Konstruktionsvorschriften erziehen zu strukturellem
Denken. Die Bildung strukturellen Denkens ist ein wichtiges Lernziel des Geometrieunterrichts.



