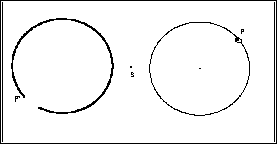Die Punktspiegelvorschrift ist eine Kongruenzvorschrift
- Wir lassen den Urpunkt
P auf der ganzen Zeichenebene wandern. Stets gibt es auch einen Punkt P' auf
der Zeichenebene, der entsprechend wandert. Die Punktspiegelvorschrift bildet
die Zeichenebene auf sich ab.
- Kommt dabei der
Urpunkt P auf den Spiegelpunkt S zu liegen, so liegt auch P' auf S. Der Spiegelpunkt
ist der einzige Fixpunkt der Punktspiegelvorschrift.
- Wandert P an die
Stelle von P', so wandert P' an die Stelle von P. Die Punktspiegelvorschrift
ist wechselseitig.
- Wir spiegeln ein
Dreieck an einem Punkt S (die drei Ecken einzeln punktspiegeln und auf die Bildpunkte
das Makro Dreieck anwenden). Damit
definieren wir das Makro Punktspiegeln-Dreieck:
Eingabeobjekte: Spiegelpunkt
S, Urdreieck ABC
Zielobjekt: Bilddreieck
A'B'C'
Den
Spiegelpunkt und das Urdreieck variieren. Dabei soll der Spiegelpunkt außerhalb/innerhalb
des Dreiecks, auf einer Seite oder in einer Ecke liegen.
|
- Wir messen
die Seitenlängen und Eckenwinkel (zuerst markieren!) von Ur- und Bilddreieck
und beobachten: Ur- und Bildstrecken sind gleichlang, Ur- und Bildwinkel
sind gleichgroß, Ur- und Bildreiecke sind deshalb deckungsgleich (kongruent).
Die Punktspiegelvorschrift ist längentreu und winkeltreu,
sie bildet Dreiecke auf kongruente Dreiecke ab.
- Beim Drehen
von Geraden haben wir festgestellt, daß bei einem Drehwinkel von 18O Grad,
Ur- und Bildgeraden zueinander parallel sind. Das wollen wir uns noch
einmal genauer ansehen. Dazu definieren wir zunächst das Makro Punktspiegeln-Gerade:
Eingabeobjekte: Spiegelpunkt
S, Punkte A und B auf g
Zielobjekte: Bildgerade
g'
|
 |
|
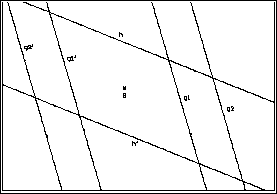
Jetzt
zeichnen wir eine "Gerade durch 2 Punkte" g1 und konstruieren
eine dazu parallele Gerade g2; g1 und g2 bilden zusammen einen Streifen,
den wir an S spiegeln. Außerdem zeichnen wir eine "Gerade" h
mit 2 "Punkten auf Objekt", (damit wir die Gerade ebenfalls
an S spiegeln können) und ihre Bildgerade h'. Anschließend variieren
wir die Figuren, indem wir g1 drehen und h parallel verschieben. Wir beobachten:
g1' ist stets parallel zu g1, g2' ist stets parallel zu g2 und zu g1',
h' ist stets parallel zu h. Gehen die Geraden g1, g2 oder h durch den
Spiegelpunkt S, dann sind sie gleich ihren Bildgeraden g1', g2' bzw. h'.
Zusammenfassend:
Jede
Bildgerade ist parallel zu ihrer Urgeraden.
Jeder
Streifen wird wieder auf einen (sogar dazu parallelen) Streifen abgebildet.
Jede
Gerade durch den Spiegelpunkt ist eine Fixgerade.
|
 |
Die
erste dieser drei Eigenschaften ist so wichtig, daß man ihr einen eigenen Namen
gegeben hat. Man sagt: Punktspiegeln ist eine perspektive Vorschrift.
|
- Mit Hilfe
der zweischrittigen Ortslinien-Strategie stellen wir schließlich fest:
Punktspiegeln ist kreistreu. Außerdem beobachten wir beim
Markieren der Bildfigur mit der Option Ortslinie: Punktspiegeln ist
orientierungstreu.
Zuletzt definieren wir das Makro Punktspiegeln-Kreis:
Eingabeobjekte: Spiegelpunkt
S, Kreismittelpunkt M, Kreispunkt A
Zielobjekt:
Bildkreis k'
|
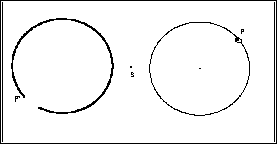 |