
In diesem Beitrag möchte ich dir eine Anwendung beschreiben, die die Bereiche
der Mathematik und Physik verbindet. Es geht um das Aussehen der Bahn eines
Balles oder einer Kanonenkugel. Vielleicht hast du ja erste Vorstellungen, wie
sich ein Ball durch die Luft bewegt, wenn man ihn wirft. Ein realgeschichtlicher
Bezug streift kurz den historischen Werdegang der heutigen Erkenntnisse und
soll zu eigenen Untersuchungen anregen, denn nur so wirst du irgendwann den
Triumph erlangen und an den Errungenschaften der Wissenschaften teilhaben.

Interessant ist sicherlich auch das Kanonenwettschießen, das in der Geschichte tatsächlich stattgefunden hat, um Theorien zu bestätigen oder zu wiederlegen. Ein Wettwerfen mit deinen Freunden zu diesen Fragestellungen wird sicher auch den letzten Maulwurf aus seinem Bau treiben:

Im Mittelalter stellte man sich vor, dass die Bahn eines Balles geradlinig in Schussrichtung verläuft. Wenn dann irgendwann seine Geschwindigkeit so weit absinkt, bis sie gleich Null ist, dann würde der Stein senkrecht auf die Erde fallen.

Niccolò Fontana (Tartaglia) (1499 Brescia bis 1557 Venedig) lebte im heutigen Italien und wurde bereits als Kind bei der Eroberung von Brescia durch die Franzosen im Jahre 1512 durch einen Säbelhieb so stark verletzt, dass er von da an stotterte. Deshalb hieß er auch Tartaglia, das ist italienisch und heißt der Stotterer. Trotz seiner Herkunft aus armen Verhältnissen und einer kurzen Schulausbildung trug Tartaglia zur Erkenntnisgewinnung in der Physik und Mathematik bei. Er war zum Beispiel als Erster in der Lage allgemeine kubische Gleichungen durch eine von ihm entwickelte Formel zu lösen. Vorher war das nur für spezielle kubische Gleichungen möglich. In der Schrift "La Nova Scientia" beschrieb Tartaglia 1537 seine Vorstellungen von der Geschossbahn einer Kanonenkugel. Er dachte, dass sich die Kanonenkugel nach Verlassen des Geschützrohres geradlinig von A nach B bewegt, dann durch die Schwerkraft in eine Kreisbahn von B bis C gezwungen wird um dann schließlich senkrecht von C nach D herunter zu fallen.
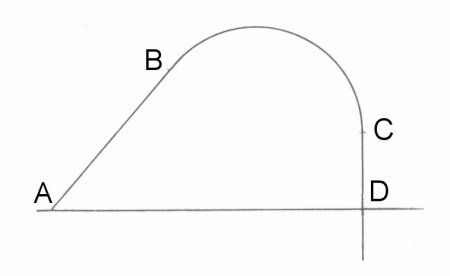
Tartaglia überlegte, dass die Schussweite der Kugel am größten sei, wenn die Kreisbahn genau die Erde wieder treffen würde, also wenn C und D ineinander fallen. Das ist nach seiner Vorstellung genau bei einem Abschusswinkel von 45° der Fall. In einem Wettschießen mehrerer "capo di bombardiere" wurden seine Vermutungen bestätigt. Sein Buch mit den Ergebnissen seiner Untersuchungen zu der Geschossbahn von Kanonenkugeln wurde noch lange in der Kanonierausbildung verwendet.
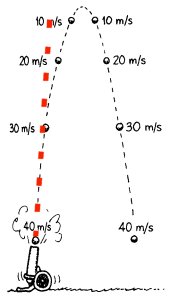
Seit Galileo Galilei (geboren am 15.2.1564 in Pisa und gestorben am 8.1.1642 bei Florenz), wissen wir, dass die Schwerkraft gleich zu Beginn auf die Kugel wirkt, wenn diese das Geschützrohr verlässt. Das bewirkt, dass sich die Kugel unterhalb der von Tartaglia gedachten Linie bewegen muss, welche auf dem Neigungswinkel der Kanone liegt. Galileo Galilei hat in mehreren Experimenten bewiesen, dass die Bahn der Kugel im luftleeren Raum einer Parabel entspricht. Ohne die Schwerkraft würde die Kugel die geradlinige rote Bahn nicht mehr verlassen. Mit der Schwerkraft setzt sich die Gesamtbahn aus einer geradlinigen gleichförmigen Bewegung in Richtung der Rohrneigung und aus der Fallbewegung zusammen.
![]()
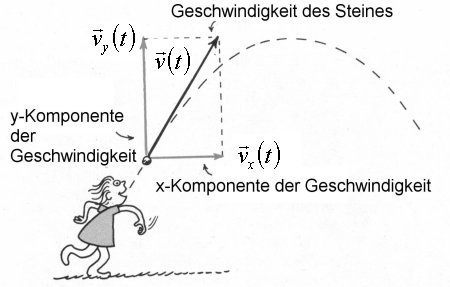
Aus der Physik wissen wir, dass für die geradlinige gleichförmige
Bewegung folgendes gilt: Man zerlegt die Bewegung ![]() in eine horizontale und eine vertikale Teilbewegung. Beide Teilbewegungen sind
gleichförmig, solange keine Luftreibung berücksichtigt wird. Wir benutzen
hierfür die Methoden der Vektorrechnung. Der Geschwindigkeitsvektor
in eine horizontale und eine vertikale Teilbewegung. Beide Teilbewegungen sind
gleichförmig, solange keine Luftreibung berücksichtigt wird. Wir benutzen
hierfür die Methoden der Vektorrechnung. Der Geschwindigkeitsvektor ![]() besitzt je eine Geschwindigkeitskomponente in x- und y-Richtung.
besitzt je eine Geschwindigkeitskomponente in x- und y-Richtung.
Mathematisch heißt das:
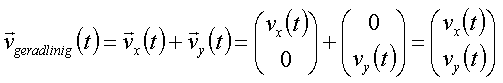 .
.
Aus der Trigonometrie wissen wir, dass ![]() und
und ![]() , wobei
, wobei ![]() die Geschwindigkeit der Kugel beim Abschuss, also zur Zeit 0 ist.
die Geschwindigkeit der Kugel beim Abschuss, also zur Zeit 0 ist. ![]() ist der Winkel zwischen dem Gesamtgeschwindigkeitsvektor und dem Vektor der
Geschwindigkeit in x-Richtung.
ist der Winkel zwischen dem Gesamtgeschwindigkeitsvektor und dem Vektor der
Geschwindigkeit in x-Richtung.
Die Fallgeschwindigkeit ![]() wirkt nur in y-Richtung und für sie gilt:
wirkt nur in y-Richtung und für sie gilt: 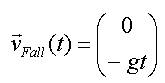
mit g als der Gravitationskonstanten und einem negativen Vorzeichen, da die
Kugel nach unten fällt. Also gilt für die Gesamtgeschwindigkeit:
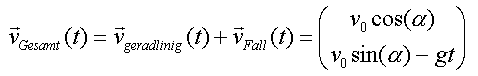
Wie lässt sich nun aber berechnen, wie hoch und wie weit die Kugel überhaupt fliegt und bei welchem Winkel die größte Höhe und Reichweite der Kugel erreicht wird?
Die Kugel hat am höchsten Punkt die Geschwindigkeit 0 in y-Richtung, denn
sie steigt nicht weiter und fällt in diesem Moment nicht. Sei ![]() die verstrichene Zeit, bis die Kugel die maximale Höhe erreicht. Also gilt:
die verstrichene Zeit, bis die Kugel die maximale Höhe erreicht. Also gilt:
![]() oder
oder ![]() .
Für die Zeit gilt also:
.
Für die Zeit gilt also: 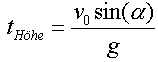 .
In dieser Zeit steigt die Kugel durch die geradlinige Bewegung um den Weg
.
In dieser Zeit steigt die Kugel durch die geradlinige Bewegung um den Weg ![]() und fällt durch die Schwerkraft um
und fällt durch die Schwerkraft um ![]() ,
legt also folgenden Weg
,
legt also folgenden Weg ![]() zurück:
zurück: 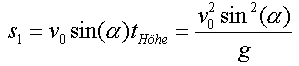
und 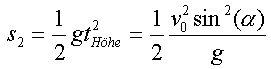 , also gilt
, also gilt 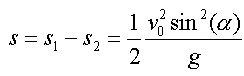 .
Der größte Wert von s wird erreicht, wenn
.
Der größte Wert von s wird erreicht, wenn ![]() am größten ist, da
am größten ist, da ![]() und g Konstanten sind. Das ist der Fall bei
und g Konstanten sind. Das ist der Fall bei 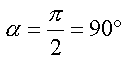 .
In Worten: Die Kugel erlangt die größte Höhe bei einem senkrechten
Schuss nach oben.
.
In Worten: Die Kugel erlangt die größte Höhe bei einem senkrechten
Schuss nach oben.
Nun befassen wir uns mit der Reichweite der Kugel. Die Kugel legt aus Symmetriegründen
den gleichen Weg vom Höhenmaximum wieder zum Boden zurück, den sie
vorher gestiegen ist. Sei ![]() die verstrichene Zeit am Ende der Bewegung, also wenn die Kugel wieder am Boden
liegt. Dann gilt deshalb:
die verstrichene Zeit am Ende der Bewegung, also wenn die Kugel wieder am Boden
liegt. Dann gilt deshalb: 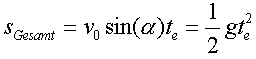 und
daraus folgt
und
daraus folgt 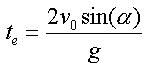 .
. ![]() ist also doppelt so groß wie die Steigezeit.
ist also doppelt so groß wie die Steigezeit.
Die Schussweite ![]() entspricht
dem Produkt aus Geschwindigkeit in horizontaler Richtung mit der Zeit
entspricht
dem Produkt aus Geschwindigkeit in horizontaler Richtung mit der Zeit ![]() :
:
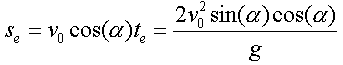 . Aus der Trigonometrie
wissen wir, dass
. Aus der Trigonometrie
wissen wir, dass ![]() und deshalb
gilt für die gesamte Schussweite:
und deshalb
gilt für die gesamte Schussweite: 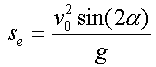 .
Dieser Wert ist am größten, wenn
.
Dieser Wert ist am größten, wenn ![]() am größten ist und das ist der Fall bei
am größten ist und das ist der Fall bei ![]() oder
oder ![]() . Man kann also am weitesten
schießen, wenn das Kanonenrohr einen Abschusswinkel von 45° besitzt.
Das ist aber auch schon das Ergebnis von Tartaglia gewesen, wenn wir uns richtig
erinnern.
. Man kann also am weitesten
schießen, wenn das Kanonenrohr einen Abschusswinkel von 45° besitzt.
Das ist aber auch schon das Ergebnis von Tartaglia gewesen, wenn wir uns richtig
erinnern.
In Realität besitzt die Erdatmosphäre eine Luftreibung. Aus diesem
Grund sieht die tatsächliche Geschossbahn etwas anders aus:
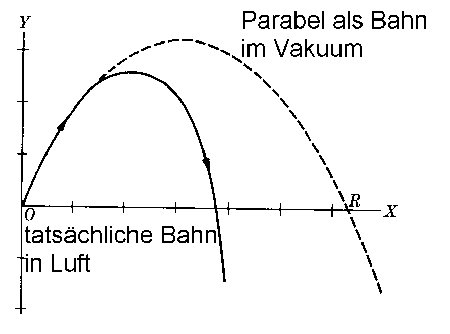
Auch hier wird man das Gefühl nicht los, dass die Bahn der vorhergesagten Bahn von Tartaglia ähnelt.