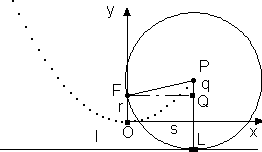
Eine Gerade l und ein Punkt F sind gegeben, wobei F nicht auf l liegt. Die Menge aller Punkte P mit der Eigenschaft |lP|=|FP| heißt Parabel. Es sind also alle Punkte, die den gleichen Abstand zum Punkt F und der Geraden l haben.
Die Gerade l heißt Leitlinie und der Punkt F heißt Brennpunkt.
Um eine Gleichung zu erhalten wählen wir die Leitlinie parallel zur x-Achse im Koordinatensystem.

Sei der Koordinatenurprung O(0, 0) im Minimum der Parabel. Dann gilt für den Brennpunkt F=(0, r). L=(s, -r), denn wenn der Kreismittelpunkt durch O geht ist |OL|=r und P=(s, r+q)=(x0, y0).
Nun gilt nach Pythagoras |PF|2=|PQ|2+|QF|2.
Da |PF|=|PL| folgt
(2r+q)2=q2+s2
4r2+4rq+q2=q2+s2
4r(r+q)=s2
![]()
![]()
Das ist aber die Gleichung einer Parabel mit der Konstanten 1/4r.